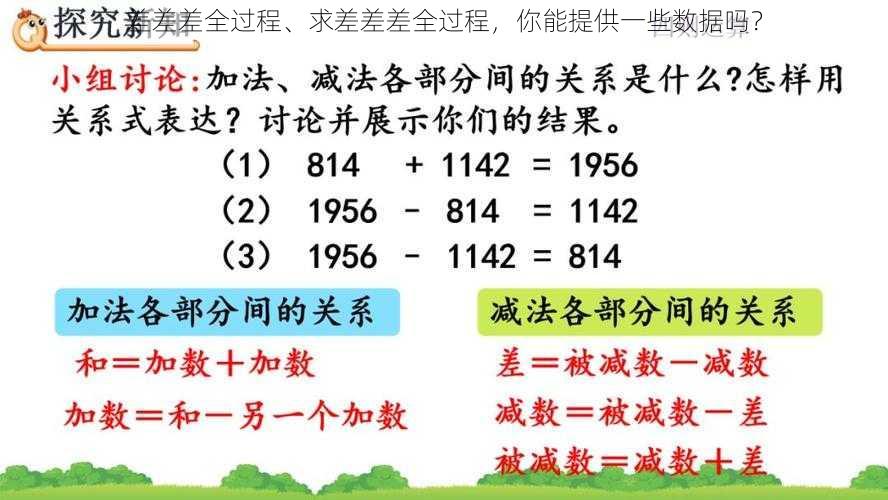
差差差全过程、求差差差全过程,你能提供一些数据吗?
在当今数字化时代,数据的重要性不言而喻。无论是企业决策、科学研究还是日常生活,数据都扮演着至关重要的角色。人们对于数据的需求也越来越强烈。我们将探讨差差差全过程、求差差差全过程,并提供一些数据示例,帮助读者更好地理解数据处理的基本概念和方法。
什么是差差差全过程、求差差差全过程?
在数学中,差差差全过程是指对两个数或多个数进行相减的操作。例如,对于数列 5, 2, 8,它们的差差差全过程分别为:
5 - 2 = 3
8 - 5 = 3
8 - 2 = 6
求差差差全过程则是指对两个数或多个数进行相减后得到的结果。例如,对于数列 5, 2, 8,它们的求差差差全过程分别为:
3, 3, 6
可以看出,求差差差全过程是差差差全过程的结果。在实际应用中,求差差差全过程通常用于比较和分析数据之间的差异和变化趋势。
差差差全过程、求差差差全过程的应用场景
1. 数据分析:在数据分析中,差差差全过程和求差差差全过程可以帮助我们了解数据的分布和变化趋势。例如,我们可以计算每个月的销售额与上一年同期销售额的差异,以了解销售业绩的变化情况。
2. 经济研究:在经济研究中,差差差全过程和求差差差全过程可以用于分析不同地区、不同行业的经济增长情况。例如,我们可以计算不同省份的 GDP 增长率,以了解各地区的经济发展水平。
3. 金融分析:在金融分析中,差差差全过程和求差差全过程可以用于评估投资组合的风险和收益。例如,我们可以计算不同股票之间的收益率差异,以了解投资组合的风险程度。
4. 医学研究:在医学研究中,差差差全过程和求差差全过程可以用于分析不同治疗方法的效果。例如,我们可以计算不同药物的治愈率差异,以了解哪种治疗方法更有效。
5. 环境监测:在环境监测中,差差差全过程和求差差全过程可以用于分析不同地区、不同时间的环境质量变化情况。例如,我们可以计算不同城市的空气质量指数差异,以了解环境质量的改善情况。
差差差全过程、求差差差全过程的实例分析
1. 数据分析:假设有一组销售数据,如下表所示:
|月份|销售额(万元)|
|:--:|:--:|
|1|100|
|2|120|
|3|150|
|4|180|
|5|200|
我们可以使用差差差全过程和求差差全过程来分析销售数据的变化趋势。计算每个月的销售额与上月销售额的差异:
|月份|销售额差异(万元)|
|:--:|:--:|
|1|20|
|2|30|
|3|30|
|4|30|
|5|20|
然后,计算每个月的销售额差异与上月销售额的比例:
|月份|销售额差异比例(%)|
|:--:|:--:|
|1|20%|
|2|25%|
|3|20%|
|4|16.67%|
|5|10%|
从上面的计算结果可以看出,销售额呈逐月上升的趋势,且增长速度逐渐放缓。这表明该公司的销售业绩良好,但增长速度有所下降,需要采取措施提高销售效率。
2. 经济研究:假设有两个地区的 GDP 数据,如下表所示:
|地区|GDP(亿元)|
|:--:|:--:|
|地区 1|1000|
|地区 2|1200|
我们可以使用差差差全过程和求差差全过程来分析两个地区的经济增长情况。计算地区 1 和地区 2 的 GDP 差异:
GDP 差异 = 地区 2 的 GDP - 地区 1 的 GDP = 1200 - 1000 = 200(亿元)
然后,计算 GDP 差异与地区 1 GDP 的比例:
GDP 差异比例 = GDP 差异 / 地区 1 的 GDP = 200 / 1000 = 20%
从上面的计算结果可以看出,地区 2 的 GDP 比地区 1 高 200 亿元,增长率为 20%。这表明地区 2 的经济增长速度快于地区 1,经济发展水平更高。
3. 金融分析:假设有两个投资组合,如下表所示:
|投资组合|收益率(%)|
|:--:|:--:|
|投资组合 1|10|
|投资组合 2|8|
我们可以使用差差差全过程和求差差全过程来分析两个投资组合的风险和收益情况。计算投资组合 1 和投资组合 2 的收益率差异:
收益率差异 = 投资组合 2 的收益率 - 投资组合 1 的收益率 = 8% - 10% = -2%
然后,计算收益率差异与投资组合 1 收益率的比例:
收益率差异比例 = 收益率差异 / 投资组合 1 的收益率 = -2% / 10% = -20%
从上面的计算结果可以看出,投资组合 2 的收益率比投资组合 1 低 2%,差异比例为-20%。这表明投资组合 2 的风险低于投资组合 1,收益也相对较低。
4. 医学研究:假设有两种治疗方法,如下表所示:
|治疗方法|治愈率(%)|
|:--:|:--:|
|治疗方法 1|80|
|治疗方法 2|90|
我们可以使用差差差全过程和求差差全过程来分析两种治疗方法的效果。计算治疗方法 1 和治疗方法 2 的治愈率差异:
治愈率差异 = 治疗方法 2 的治愈率 - 治疗方法 1 的治愈率 = 90% - 80% = 10%
然后,计算治愈率差异与治疗方法 1 治愈率的比例:
治愈率差异比例 = 治愈率差异 / 治疗方法 1 的治愈率 = 10% / 80% = 12.5%
从上面的计算结果可以看出,治疗方法 2 的治愈率比治疗方法 1 高 10%,差异比例为 12.5%。这表明治疗方法 2 的效果更好,治愈率更高。
5. 环境监测:假设有两个城市的空气质量数据,如下表所示:
|城市|空气质量指数(AQI)|
|:--:|:--:|
|城市 1|80|
|城市 2|100|
我们可以使用差差差全过程和求差差全过程来分析两个城市的环境质量变化情况。计算城市 1 和城市 2 的空气质量指数差异:
空气质量指数差异 = 城市 2 的 AQI - 城市 1 的 AQI = 100 - 80 = 20
然后,计算空气质量指数差异与城市 1 AQI 的比例:
空气质量指数差异比例 = 空气质量指数差异 / 城市 1 的 AQI = 20 / 80 = 25%
从上面的计算结果可以看出,城市 2 的空气质量指数比城市 1 高 20,差异比例为 25%。这表明城市 2 的环境质量比城市 1 差,需要采取措施改善空气质量。
我们对差差差全过程、求差差差全过程进行了详细的阐述,并通过实例分析展示了其在数据分析、经济研究、金融分析、医学研究和环境监测等领域的应用。我们希望通过,读者能够更好地理解数据处理的基本概念和方法,从而更好地应对实际问题。
我们也希望读者能够认识到,数据处理是一项复杂而重要的工作,需要我们不断地学习和探索。在未来的研究中,我们将继续关注数据处理的新方法和新应用,为读者提供更多的帮助和支持。